 POTENCIA DE LA LARINGOSCOPIA INDIRECTA INCLUIDA EN UN MÉTODO DE PREDICCIÓN DE LA DIFICULTAD DE INTUBACIÓN APLICABLE A CUALQUIER PACIENTE.
POTENCIA DE LA LARINGOSCOPIA INDIRECTA INCLUIDA EN UN MÉTODO DE PREDICCIÓN DE LA DIFICULTAD DE INTUBACIÓN APLICABLE A CUALQUIER PACIENTE.
POTENCIA DE LA LARINGOSCOPIA INDIRECTA.
Resumen
Introducción y objetivos: El objetivo de este estudio es investigar la potencia de la Laringoscopia Indirecta con el Laringoscopio Rígido de 70º como predictor de dificultad de intubación de la laringe mediante Laringoscopia Directa y como aplicar nuestros resultados a cualquier paciente.
Material y Métodos: En el preoperatorio de 300 pacientes, además de los parámetros y pruebas predictoras de vía aérea difícil habituales, se incluyó una Laringoscopia Indirecta con el Laringoscopio Rígido. Según la visión obtenida de la vía aérea superior se obtuvieron cuatro grados: 1 (cuerdas vocales visibles), 2 (comisura posterior y epiglotis visible), 3 (visión sólo de epiglotis) y 4 (ninguna estructura glótica visible). EL 3 y el 4 eran considerados predictores de dificultad de intubación. Después, bajo anestesia general, practicamos a los pacientes la Laringoscopia Directa con el laringoscopio de Macintosh. Valoramos como dificultad de intubación positivo si se necesitaban al menos tres maniobras de intubación. Se elaboró un modelo de regresión logística con fines predictivos utilizando las variables relevantes. Se aplica el modelo a cualquier paciente mediante la inserción en la barra de fórmulas en Excel de una función dada.
Resultados: Se encontró dificultad de intubación en 14 casos el 4,66 %. El modelo encontrado y sus coeficientes para confeccionarlo fueron: f(x) = -4,741 + 2,567 Laringoscopia Indirecta (3-4) + 2,323 Distancia tiromentoniana <6,5cm + 1,654 Apertura boca<3,5cm. Proporciona un resultado correcto en el 95,3 % de los casos. La probabilidad teórica (y) asociada a un paciente de encontrarnos con una dificultad de intubación es y = e f(x)/(1+e f(x)) donde x es el resultado de la ecuación de Regresión logística y extrapolándolo a Excel la función a aplicar sería =EXP(f(x)/(1+(EXP(f(x)).
Conclusiones: La Laringoscopia Indirecta fue la variable independiente con más poder predictivo (mayor coeficiente) y la función obtenida se puede aplicar a cualquier paciente.
Palabras clave: Predictor; Vía Aérea difícil; Laringoscopia indirecta; Laringoscopio rígido; Laringoscopia directa.
POWER OF INDIRECT LARYNGOSCOPY INCLUDED IN A METHOD OF PREDICTION OF INTUBATION DIFFICULTY APPLICABLE TO ANY PATIENT.
POWER OF INDIRECT LARYNGOSCOPY.
Summary
Introduction and objectives: The aim of this study isis to investigate the power of indirect laryngoscopy with the rigid 70º laryngoscope as a predictor of difficulty in intubation of the larynx by direct laryngoscopy and how to apply our results to any patient.
Material and Methods: In the preoperative period of 300 patients, in addition to the parameters and usual difficult airway predictive tests, an indirect laryngoscopy with a rigid laryngoscope was included. According to the vision obtained from the upper airway, four grades were obtained: 1 (visible vocal cords), 2 (posterior commissure and visible epiglottis), 3 (vision only of epiglottis) and 4 (no visible glottic structure). EL 3 and 4 were considered predictors of intubation difficulty. Then, under general anesthesia, we practice direct laryngoscopy with the Macintosh laryngoscope. We value as a positive intubation difficulty if at least three intubation maneuvers were needed. A logistic regression model was developed with predictive purposes using the relevant variables. The model is applied to any patient by inserting a given function into the Excel formula bar.
Results: Intubation difficulty was found in 14 cases, 4.66%. The model found and its coefficients to make it were: f(x) = -4,741 + 2,567 Indirect laryngoscopy (3-4) + 2,323 Thyromentonian distance <6,5cm + 1,654 Mouth opening <3,5cm. It provides a correct result in 95.3% of cases. The theoretical probability (y) associated with a patient of encountering an intubation difficulty is y = ef (x) / (1 + ef (x)) where x is the result of the Logistic Regression equation and extrapolating it to Excel the function to apply would be = EXP (f (x) / (1+ (EXP (f (x)).
Conclusions: Indirect laryngoscopy was the independent variable with more predictive power (higher coefficient) and the function obtained can be applied to any patient.
Keywords: Predictor; Difficult airway; Indirect laryngoscopy; Rigid laryngoscope; Direct laryngoscopy.
Introducción.
Es conocido, antes de la práctica de una anestesia general (AG), la importancia de la predicción de encontrarnos con una vía aérea difícil (VAD), que incluye: la dificultad de ventilación con mascarilla facial (DVMF), la dificultad de visión de la laringe (DVL) y la dificultad de intubación orotraqueal (DIO), cuando se realiza la Laringoscopia Directa (LD). Además de los métodos habituales y conocidos de predicción de VAD antes de la aplicación de una AG, se ha incluido por algunos autores la realización de una Laringoscopia Indirecta (LI), con instrumentos como el larynx-illuminator1 (una variante del espejo laríngeo), el espejo laríngeo2 o el laringoscopio rígido3, para así obtener una visión de la vía aérea superior (VAS) y mejorar la previsión de una VAD. En un artículo4 se estudia la influencia de las anomalías diagnosticadas mediante LI en la predicción de la DIO, pero no se incluyen entre las variables a investigar la LI y los grados de visión obtenidos.
En el artículo3 que incluye la LI entre las variables a investigar, se estudia el método que nos aproxima mediante una fórmula matemática a la predicción de DVL en los pacientes, pero no está estudiado ese método como predicción de una DIO y como aplicarlo a cualquier paciente fuera del estudio.
El objetivo principal de este artículo es investigar la potencia de la LI con el Laringoscopio Rígido de 70º, como predictor de la DIO cuando se realiza la LD bajo AG. Para ello se elaboró un modelo de regresión logística con aquellas variables relevantes de entre todos los predictores. El objetivo secundario es dar a conocer un método para aplicar nuestros resultados a cualquier paciente y en cualquier momento.
Métodos.
El protocolo de actuación fue el ya expuesto en artículos anteriores4, 5. El día programado para la intervención, en el área quirúrgica, el anestesiólogo en presencia del paciente rellenaba un hoja de protocolo que incluía datos de la consulta de preanestesia como: la edad, el sexo, el IMC, (> 30 obesidad) predictores demográficos, y la evaluación de la vía aérea. Ésta evaluación consistía en explorar los siguientes predictores: a) la escala de Mallampati modificada6, las clases 3 (visibilidad sólo del paladar blando y base de úvula) y 4 (sólo es visible el paladar duro) se consideran predictoras de DVL y DIO, b) la DTM (normal ≥ de 6,5 cm), c) la apertura de la boca (normal > 3,5 cm), cifras inferiores de ambas medidas son consideradas de pronóstico de DVL y DIO, d) la circunferencia del cuello (>43 cm indica DVL y DIO) y e) test de movilidad cervical (buena movilidad cervical: 1, disminución movilidad cervical: 2). También se incluyó en la hoja de protocolo si el paciente padecía roncopatía o anomalías tipo retrognatia.
Después, el paciente se pasaba en la camilla a la sala adjunta al quirófano donde iba a ser intervenido, ahí, se encontraba en una torre el Laringoscopio Rígido 70º 8,5 mm (Sopro-Comeg Alemania®; número de referencia 162 081 685). Tras preparar el equipo se sentó al paciente en una silla, de espaldas a la pantalla del monitor, con la cabeza en extensión y se procedió a realizarle la LI7. Se anotaron en la hoja de protocolo, tras la LI, las características de la exploración que se clasifican en cuatro grados1: 1) cuerdas vocales visibles, 2) Se observa la comisura posterior y la epiglotis, 3) Se ve sólo la epiglotis; 4) No hay visible ninguna estructura glótica. Se considera prueba positiva (predictora de DIO) los grados 3 y 4.
Además se registraba el hallazgo de anomalías como: epiglotis abarquillada, flácida o hipertrofiada, la existencia de amìgdalas linguales, tumoraciones en la vía aérea superior o cualquier otra que fuese sólo visible con la LI. No obstante, si las anomalías contraindicaban la intubación con LD, se recomendaba intubación con fibroscopio y estos pacientes eran excluidos del estudio.
Posteriormente, el paciente pasó al quirófano, allí, después de ser premedicados con 0,05 mg de fentanilo y de aplicarles O2 al 100 % durante unos 3 minutos a través de la mascarilla facial, se les administró propofol 2 mg/kg y succinilcolina 1mg/kg, se ventilaba con la mascarilla facial, a continuación, el anestesiólogo (con más de cinco años de experiencia y distinto al que había realizado la LI, por lo que desconocía la valoración de ésta, aunque si conocía todas las demás pruebas de predicción de DIO) procedió usando el laringoscopio de Macintosh del tamaño adecuado, a practicar la maniobra de intubación. La visión de la LD obtenida se clasificó según la graduación de Cormak- Lehane8 en cuatro grados. En caso de no observar el orificio de la glotis (Cormak- Lehane: III-IV) se procedía a realizar presión cricotiroidea (se registraba esta maniobra), si con ello se observaba el orificio de la glotis, se intubaba el paciente. Si no se conseguía una buena visión y se necesitaban al menos tres maniobras con el laringoscopio de Macintosh, se consideraba el caso como de DIO y si era necesario, se utilizaban los instrumentos adecuados (guía de Eschmann, Glidescope o Airtraq u otros) y se registraba el evento.
En primer lugar, vamos a explorar la asociación y estimar la significación estadística que existe entre los predictores clínicos, demográficos y la LI, con la DIO observada mediante LD (Tabla 1). Hacemos notar que todas son variables categóricas. Para valorar la potencia de la LI como predictor de la DIO e investigar qué variables explicativas o independientes (predictores clínicos, demográficos y LI) se relacionan con la variable respuesta o dependiente DIO, se realizó un análisis de regresión logística. Una vez practicados el análisis de regresión logística con los coeficientes encontrados, se realizó un modelo f(x) en cada caso, para determinar la probabilidad teórica (y) asociada a un paciente de encontrarnos con una DIO, Tabla 2. y = e f(x)/(1 + e f(x)) y extrapolándolo a Excel la función a aplicar sería==EXP(f(x)/(1+(EXP(f(x)).
Con la probabilidad teórica o pronosticada en cada paciente de encontrarnos ante una DIO se puede confeccionar la curva COR (característica operativa del receptor), que proporciona la medida global del poder de la ecuación valorando el área bajo la curva obtenida, al representar la sensibilidad y especificidad del modelo. También se realizó un gráfico de cajas para observar las diferencias entre las cifras de probabilidad pronosticada entre los pacientes con DIO y sin DIO. Los datos se analizaron con el programa SPSS 15® para Microsoft Windows®.
Los resultados se expresan como media, mediana (rango) y frecuencia. Se utilizó la prueba t de Student para muestras independientes con las variables continuas y el test χ2 o el test de Fisher con las variables cualitativas. Se comprobó la normalidad de las variables continuas con el test de Kolmogorov-Smirnov. El valor de significación estadística se asumió cuando p<0,05.
Resultados
Se incluyeron en el estudio 324 pacientes de los que se excluyeron 23 a los que no se les pudo realizar la LI por náuseas o tos (7 %) y uno porque presentaba un tumor de epiglotis y se indicó intubación orotraqueal con el nasofibroscopio en paciente despierto. Para poder realizar la intubación orotraqueal fue preciso practicar presión cricotiroidea en 57 pacientes (19 %) y en 14 pacientes (4,7 %) se realizaron al menos 3 intentos de intubación orotraqueal.
En la Tabla 1 se observan las 12 variables todas categóricas introducidas en el programa y su significación estadística. En la Tabla 2 se pueden observar los resultados del análisis de regresión logística, la relación y la potencia de las variables independientes con la variable dependiente DIO. En la Tabla 3 se contemplan las cifras de probabilidad pronosticada obtenidas de los diferentes pacientes y su par asociado de sensibilidad y 1-especificidad. Con ellas como coordenadas se obtiene la curva ROC. En la Tabla 4 se ven las cifras de probabilidad pronosticada que aparecen después de estudiar los 300 pacientes y número de veces que se repiten.
En la figura 1 se puede ver la curva ROC obtenida al contrastar las cifras de probabilidad pronosticada de la Tabla 3 con la variable dependiente DIO. En la figura 2 se distinguen las dos cajas que reflejan la distribución de las probabilidades pronosticadas en los casos con DIO y en los casos sin DIO. Se visualizan las medianas y su diferente altura en cada caja y los valores periféricos (outliers) en la primera.
Para aplicar el modelo a cualquier paciente con los coeficientes obtenidos en la tabla 2, lo haríamos así: tenemos un paciente que presenta una LI de 2, una DTM < 6,5 cm y una apertura de boca boca <3,5cm.: f(x) = -4,741+ 2,323 DTM < 6,5 cm + 1,654 Apertura boca <3,5cm. Realizamos la operación y el resultado es = -0,764. Abrimos Excel vamos a la barra de fórmulas e insertamos la función fx=EXP(-0,764)/(1+EXP(-0,764)). Resolvemos y nos da como resultado: 0,317778454. Muy similar al resultado observado en la Tabla 4 en 6 pacientes: 0,31762. con esas mismas variables en la ecuación:
Tabla 1. Variables introducidas en la ecuación.
| Puntuación | gl | Sig. | ||
| Variables | sexo | 0,512 | 1 | 0,474 |
| roncador | 0,648 | 1 | 0,421 | |
| retrognatia | 14,923 | 1 | 0,000 | |
| DTM | 28,340 | 1 | 0,000 | |
| Aperturaboca | 7,535 | 1 | 0,006 | |
| Grosorcuello43 | 0,012 | 1 | 0,911 | |
| IMCmayor30 | 1,090 | 1 | 0,296 | |
| MovilidadcervicaL | 3,645 | 1 | 0,056 | |
| PronosticodificintLI | 25,301 | 1 | 0,000 | |
| Previstomall | 7,035 | 1 | 0,008 | |
| Epaba | 4,293 | 1 | 0,038 | |
| AmigLin | 1,982 | 1 | 0,159 | |
| Estadísticos globales | 60,697 | 12 | 0,000 | |
Tabla 2. Predictores clínicos independientes de la dificultad de intubación orotraqueal DIO.
| B | Sig. | Exp(B) | I.C. 95% para EXP(B) | |||
| Inferior | Superior | |||||
| Paso 3c | DTM(1) | 2,323 | 0,000 | 10,204 | 2,934 | 35,490 |
| Aperturaboca(1) | 1,654 | 0,041 | 5,227 | 1,073 | 25,467 | |
| Pronosticodificint(1) | 2,567 | 0,000 | 13,022 | 3,612 | 46,949 | |
| Constante | -4,741 | 0,000 | 0,009 | |||
Tabla 3. Coordenadas de la curva ROC.
Variables resultado de contraste: Probabilidad pronosticada
| Probabilidad pronosticada | Sensibilidad | 1 – Especificidad |
| 0,0000000 | 0,000 | 0,000 |
| 0,0261383 | 0,780 | 0,143 |
| 0,0626946 | 0,808 | 0,143 |
| 0,0919027 | 0,881 | 0,214 |
| 0,2098290 | 0,969 | 0,500 |
| 0,3451326 | 0,979 | 0,714 |
| 0,4547929 | 0,986 | 0,714 |
| 1,0000000 | 1,000 | 1,000 |
El punto de corte se sitúa en la probabilidad pronosticada de 0,0626946, sen= 0,808, esp= 0,143.
Tabla 4. Cifras de probabilidad pronosticada y Nº de veces que aparecen.
| Probabilidad pronosticada | N | |
| Dificultad intubacion | 0,00865 | 225 |
| 0,04363 | 8 | |
| 0,08176 | 22 | |
| 0,10204 | 29 | |
| 0,31762 | 6 | |
| 0,37265 | 2 | |
| 0,53694 | 8 |
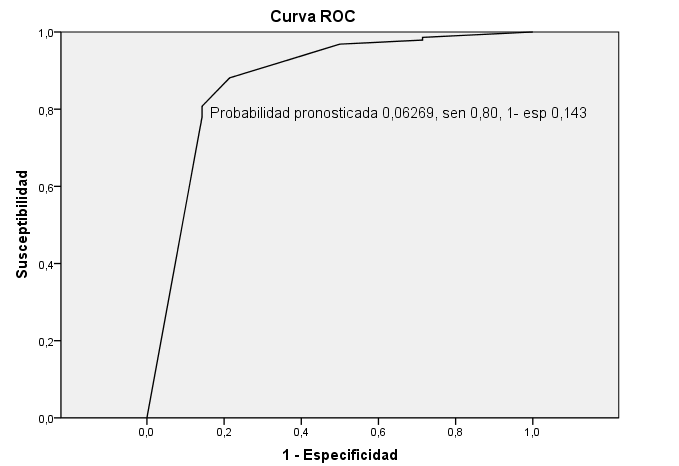
Figura 1. Curva de función operativa (ROC) de la probabilidad pronosticada: y, obtenida en cada paciente, de encontrar una DIO. Se marca el punto de corte más cercano al ángulo superior izquierdo, al que le corresponde una probabilidad pronosticada de 0,06269, con una sensibilidad del 80 % y una cifra de 1-especificidad del 14 %. El área bajo la curva es del 89 %, sen = sensibilidad, esp = especificidad. Figure 1. Operative function curve (ROC) of the predicted probability: y, obtained in each patient, to find a DIO. The cutoff point closest to the upper left angle is marked, which corresponds to a predicted probability of 0.06269 , with a sensitivity of 80% and a figure of 1-specificity of 14%. The area under the curve is 89%, sen = sensitivity, esp = specificity.
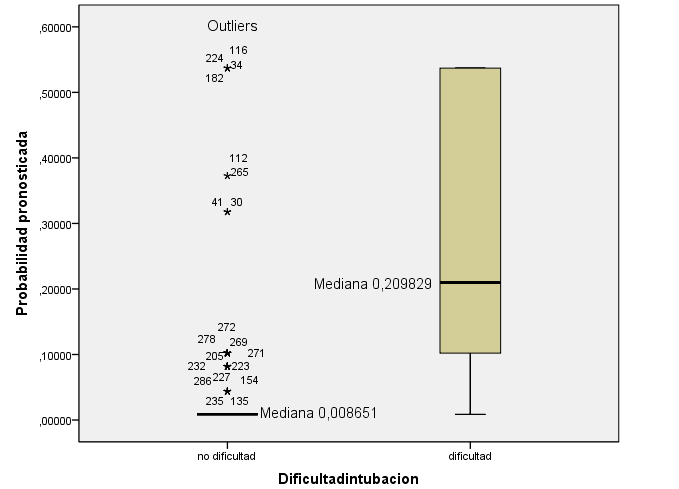
Figura 2. Se advierte en la primera caja que 8 pacientes sin DIO presentan una probabilidad pronosticada por encima de la mediana de los pacientes con DIO. En la segunda caja muestra la existencia de pacientes con DIO con una probabilidad muy baja. Figure 2. It is noted in the first case that 8 patients without IHD have a predicted probability above the median of patients with IOD. In the second box shows the existence of patients with IOD with a very low probability.
Discusión.
En la tabla 1 se contemplan todas las variables categóricas que hemos introducido en el análisis de regresión logística para obtener la ecuación, se observa que no todas tienen una significación <0,005. Se podrían haber introducido en el análisis de entre todas sólo las variables significativas, pero hemos comprobado que aunque los coeficientes de la ecuación cambian, las cifras de la (y) pronosticada, en cada paciente, son las mismas que si introducimos todas las categóricas como es nuestro caso, la curva ROC y las coordenadas para su realización también son las mismas y también lo es el diagrama de cajas que se obtiene.
En la tabla 2 podemos ver que la odd ratio (Exp(B)) de la LI es 13,02 (esto significa que un paciente con LI = 3-4 tendría 13 veces más riesgo de presentar una DIO que un paciente con una LI = 1-2). Esta cifra se obtiene elevando el número e, al coeficiente B (e2,567 = 2,7172 2,567 = 13,022). Y esta cifra es la mayor de la tabla.
En la Tabla 3 se observa que para una misma cifra de 1-especificidad: 0,143 se corresponden dos distintas cifras de sensibilidad, se escoge como punto de corte, aquella cifra de probabilidad pronosticada con sensibilidad más alta y más cercana al ángulo izquierdo del gráfico (Figura 1), en este caso correspondería a y =0,0626946. La curva ROC (Figura 1) enfrenta la sensibilidad en ordenadas frente a 1-especificidad, o sea el porcentaje de verdaderos positivos frente a los falsos positivos, para los distintos valores de y (probabilidad pronosticada). En el ángulo superior izquierdo se situaría la cifra en la que todos los pacientes con DIO son detectados, mientras que ninguno sin DIO es falsamente positivo. El mejor punto de corte correspondería a aquella cifra de ·”y”, que más se acerque al ángulo superior izquierdo, en nuestro caso correspondería a y = 0,0626946, en la que el 80 % (sensibilidad) de los pacientes con DIO son detectados, con una proporción de falsos positivos del 14 %.
En la figura 2 se observa en la caja de pacientes no incluidos en el grupo de DIO los outliers , de los cuales ocho presentan una “y” por encima de la mediana de lospacientes con DIO. Cuatro presentan una cifra de y = 0,53694 que es una cifra de probabilidad pronosticada alta, pero sin embargo, no presentan una DIO, son los falsos positivos, esto disminuye el valor predictivo positivo de la prueba (VPP). Repasando las historias de estos pacientes observamos que en realidad todos precisaron presión cricotiroidea para lograr la intubación y 2 intentos, pero al no llegar a los 3 intentos de intubación orotraqueal para conseguirlo, no fueron incluidos en el grupo de DIO. Por otro lado, se observa pacientes con DIO presentan una cifra de y = 0.00865, igual a la mediana de los sin DIO.
Repasando los historiales clínicos observamos que eran dos pacientes el nº 77 es un varón de 19 años con todas los predictores de VAD normales y una LI de 2, pero que presentaba una epiglotis abarquillada que posiblemente al relajar el paciente para la maniobra de IO, dificultó la visión de la glotis, (Cormack- Lehane III) se intubó con maniobra de presión cricotiroidea y fiador metálico al cuarto intento; el nº 243 era un varón de 67 años, sólo presentaba como predictor de VAD que era roncador y Mallampati de 3, la LI era de 2, presentaba un Cormak- Lehane de I, aunque presentaba dientes únicos en arcada superior que impedían la visión de la glotis y la intubación precisó cuatro intentos9. Se observa que los dos pacientes sufrían anomalías que dificultaban la intubación y que no estaban incluidas entre las variables resultantes tras el análisis de regresión logística.
Todo esto viene a explicar el porqué de la diversidad que existe en cuanto al porcentaje de pacientes que los autores en los diferentes trabajos encuentran con DIO. Incluso depende, aunque el protocolo para su definición fuese el mismo en todos los ensayos de uno u otro anestesiólogo y en un mismo especialista de su habilidad en ese momento. El artículo4 y este coinciden en incluir la DTM y la apertura de la boca, como variables independientes en el análisis de regresión logística. Sólo varían en la tercera variable que en el artículo4 fue la presencia de anomalías y en este la LI. En el artículo3 se demostró que las variables que la apertura de la boca no influye en la visión de la LI y la DTM <6,5 tampoco era una variable significativa, variables que si influían en la DVL bajo LD. Luego un paciente con estas 2 alteraciones y además con LI de 3 ó 4, presenta alteraciones en la visión con los dos instrumentos.
Esto nos indica que un paciente que presente alteraciones en las tres variables tiene grandes posibilidades de presentar una DIO. En nuestro estudio ninguno de nuestros pacientes presentó alteraciones en las tres variables. En caso de tenerlas su “y” pronosticada sería de 0,8585137. Para aplicar el modelo a cualquier paciente creemos que el programa Excel es el más práctico pues está incluido en la mayoría de ordenador personales.
Conclusión.
La LI fue la variable independiente con más poder predictivo (mayor coeficiente) y la función obtenida después del análisis de regresión logística se puede aplicar a cualquier paciente.
Bibliografía.-
1.-Yamamoto K, Tsubokawa,T, Shibata K, Ohmura S, Nitta S, Kobayashi T. Predicting difficult intubation with indirect laryngoscopy. Anesthesiology 1997; 86 (2): 316-21.
2.-Trujillo FM, Fernández JJ. , Moncaleano JA. Laringoscopia indirecta como predictor de entubación difícil. Rev Col Anest. 2004; 32 (2):105-114.
3.- Sánchez Morillo J, Estruch Pérez MJ, Hernández Cádiz MJ, Tamarit Conejeros JM, Gómez Diago L, Richard Aznar M. La laringoscopia indirecta mediante laringoscopio rígido de 70º como valor predictivo de la dificultad de visión de la laringe. Acta Otorrinolaringol Esp. 2012; 63(4):272-9.
4.-Sánchez-Morillo J, Gómez-Diago L, Hernández-Cádiz MJ, Balaguer-Doménech J, Barber-Ballester G, Richart-Aznar M. Influencia de las anomalías faringolaríngeas diagnosticadas mediante laringoscopia indirecta en la predicción de la dificultad de intubación. Rev Esp Anestesiol Reanim. 2015;62(5):245-52.
5.-Sanchez Morillo J, Solaz Roldán C, Mompó Romero L, Soliveres Ripoll J. Utilización de la laringoscopia indirecta con laringoscopio rígido en la preanestesia de 2 pacientes con Mallampati 4 para estudiar la vía aérea y decidir la técnica de intubación. Rev Esp Anestesiol Reanim. 2009; 56: 126-7.
6.-Lee A, Fan LT, Gin T, Karmakar MK, Ngan Kee WD. A systematic review (meta-analysis) of the accuracy of the Mallampati tests to predict the difficult airway. Anesth Analg 2006; 102 (6): 1867-78.8.
7.-Remacle M, Lawson G, Giovanni A. Exploration du larynx. En Choppin D. Encycl Méd Chir. Oto-rhino-laryngologie, París: Elsevier Masson SAS. 2005; 20-635-A.
8.-Lee A, Fan LT, Gin T, Karmakar MK, Ngan Kee WD. A systematic review (meta-analysis) of the accuracy of the Mallampati tests to predict the difficult airway. Anesth Analg 2006; 102 (6): 1867-78.8.
9.-García Guiral M, García-Amigueti F, Ortells-Polo M.A, Muiños-Haro P, Gallego-González J, Carral-Olondris J.N. Relación entre el grado de laringoscopia y de dificultad de intubación. Rev Esp Anestesiol Reanim. 1997.
